As we discussed in our previous post, the first step when tackling a multiphase CFD problem is to identify the key characteristics of your physical system. Once you've done this (using our checklist if you are still new to multiphase CFD), you can begin to make informed decisions on what multiphase modelling approaches to use.
We've compiled the following guidelines based on the decades of experience that LEAP has developed while helping customers in Australia and New Zealand to solve multiphase CFD problems, particularly companies and researchers in the minerals, process and energy industries:
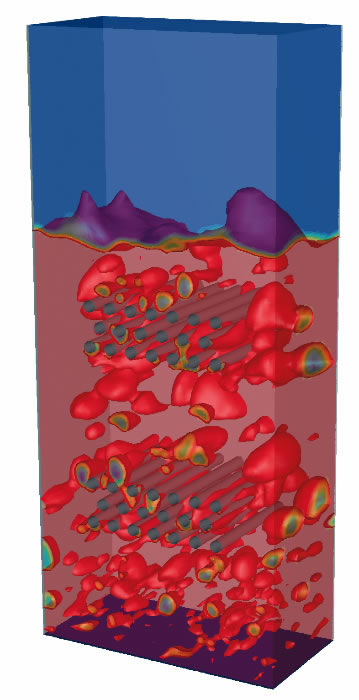
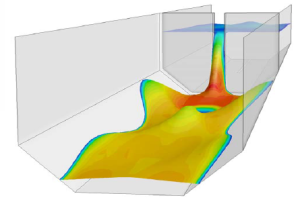
[1] If your problem involves a distinct free surface between two fluids (typically liquids), then the "Free surface" model in CFX or "Volume of Fluid / VOF" model in Fluent should be selected. Both of these methods allow an interface to be solved in steady-state (if it achieves an equilibrium state) or tracked over time in a transient simulation.
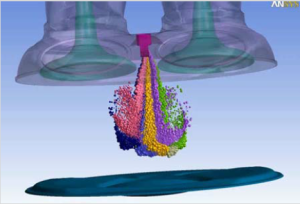
[2] If your system involves a dilute system of droplets or particles (maximum volume fractions less that ~5%) and you need to track typical trajectories to follow physical processes (such as drying, evaporation, combustion etc.), then you need to use a Lagrangian approach: this is termed the Discrete Particle Model (DPM) in Fluent & the Particle Transport model in CFX. Both codes have an extensive range of in-built models related to the particle physics, so we encourage you to review these options in the manual before you start and contact LEAP if you have specific questions.
[3] If your Stokes number is small, then the particles will quickly reach equilibrium with the fluid flow and travel at their terminal velocity. In this case, the Mixture model in Fluent or the Algebraic Slip Model (ASM) in CFX are good choices for a balance of accuracy and speed. The reason that these models greatly reduce computational time is that they only solve a single momentum equation and the other velocities are obtained by calculating the particle slip velocity.
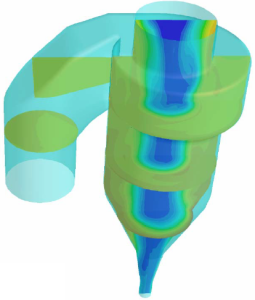
[4] If your Stokes number is larger, then an Eulerian model will be needed. An Eulerian multiphase model will solve a separate velocity field for each phase, which is the most general approach and allows complete freedom as to the behaviour of each phase within your domain.
[5] If you have solid particles present, then you will need to understand the maximum packing density for your system (incorporating particle shape and size distribution), and then decide how you are going to enforce it. If the packing limit of your particles is not likely to be reached (or is unimportant to your simulation), then the Eulerian Granular models can be used which are based on solids pressure models and kinetic theory. If you want to track particle trajectories more accurately including mechanistic physics of the solids build-up (and account for complex interactions/collisions between particles), we recommend that you use the Dense Discrete Particle (DDPM) model in ANSYS Fluent and combine it with the Discrete Element Model (DEM). This approach allows you to respect the maximum packing limit (as it considers the voidage of the Lagrangian model within the Eulerian phase) and account for the particle-particle interactions/collisions.
[6] In all of these approaches, you will need to choose the constitutive physics models for drag, lift, turbulent dispersion etc. that are appropriate for your problem. The User Guides for CFX and Fluent contain a lot of useful information to help in this process. Often it is a good strategy to start with the simple models, and incrementally activate models that incorporate more physics so that you can understand the effect they have on the accuracy of your solution.
[7] Transient or steady-state? Even though you may be looking for a steady-state solution, multiphase flows are often complex and in many cases we find that you can only approach a pseudo-steady-state result using a transient simulation technique. Keep this in mind and if you find that convergence to a steady-state solution is proving difficult, approach it via a transient simulation.
[8] If you decided that gravity was important, make sure you include it in your simulation. You will need to specify a reference density, which should be that of the lightest phase. The inclusion of gravity will also sets some conditions on how you specify your boundary conditions. If you have a separated flow leaving a pipe which is orthogonal to the gravity vector, the pressure is not constant (so ideally you would account for the hydrostatic pressure component). A common workaround is to place a 90 degree elbow downstream of the outlet which allows you to set a constant average pressure boundary condition without affecting the results in the key region of interest.
[9] It is important to give physically consistent initial conditions. If you have a fluid mixture present, then calculate the pressure so that you can set a consistent pressure field that includes the remaining hydrostatic component after the reference density is subtracted.
[10] If you are using the DPM / Lagrangian model, start solving your model initially with a small mass flow rate and a few hundred trajectories so that you can check everything is set up correctly. Doing this sanity check early on is much more efficient than waiting for the full simulation to complete only to find out there was a simple setup error.
We hope that these guidelines are enough to get started with your first multiphase CFD simulations. If you require more general assistance, please consider attending an appropriate training course or feel free to ask a specific question below.