This blog series focuses on a common question: What y+ should I use in my simulations? This is Part 2 in the series – Resolving each region of the boundary layer.
What y+ should I use? Part 2 - Resolving each region of the boundary layer
Archives for turbulence modelling
What y+ should I use? Part 1 - Understanding the physics of boundary layers
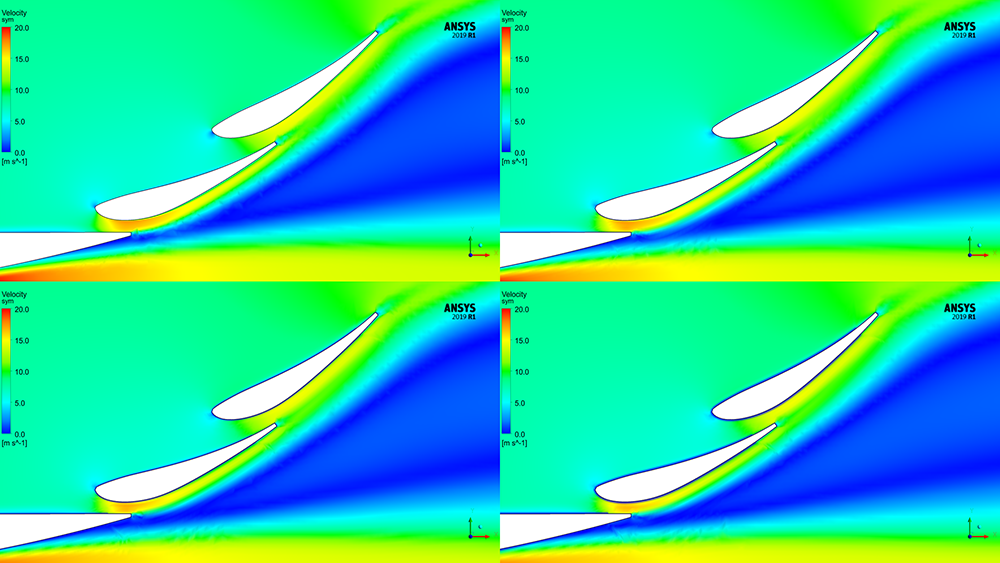
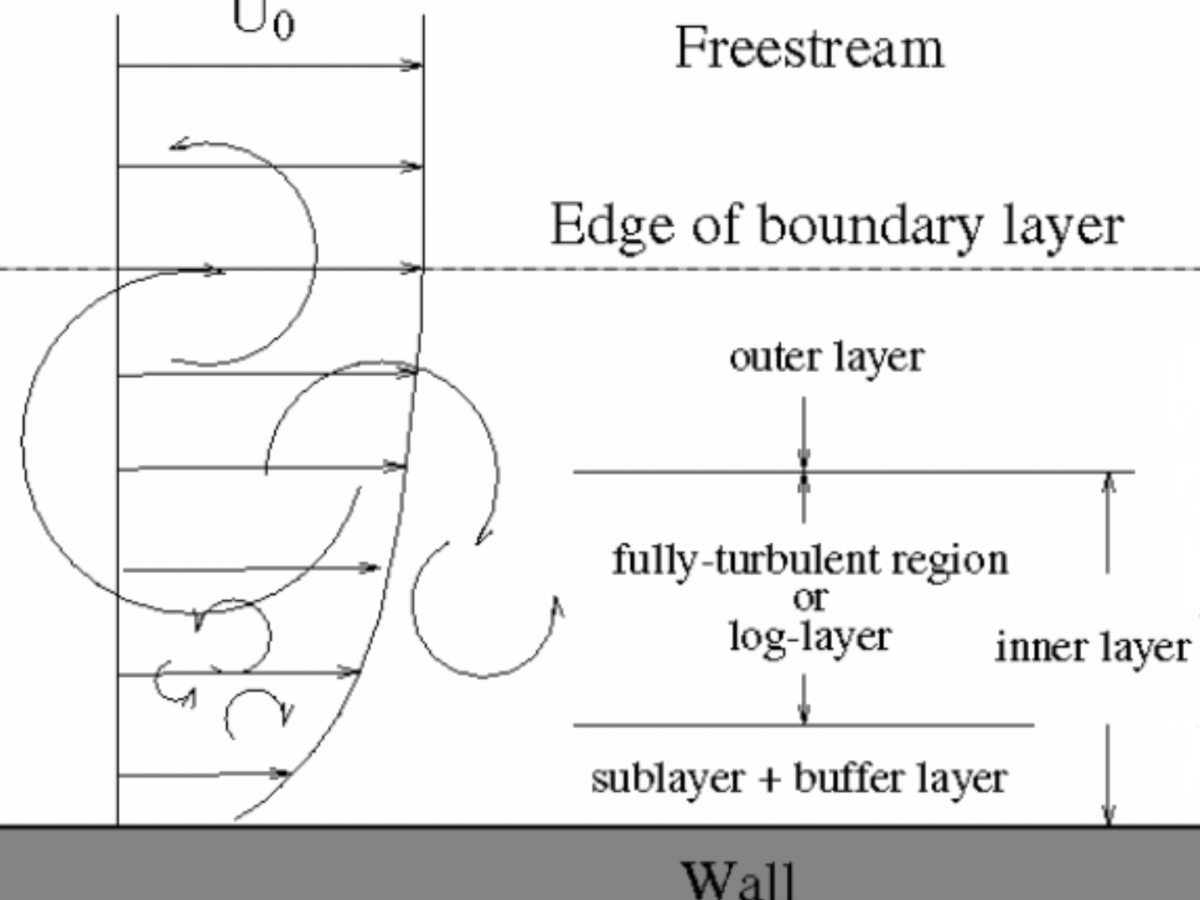
This blog series focuses on a common question: What y+ should I use in my CFD simulations? This first post is designed to help you understand the physics of boundary layers in relation to CFD meshes and Y+ values.
How can CFD help us better understand the physics of reverse-swing bowling?
In cricket, reverse swing bowling is much talked-about but often misunderstood. Conditions in the much anticipated 2019 Ashes cricket series between Australia and England are expected to be conducive to reverse-swing bowling. Let's use some CFD examples to help better understand the science of reverse-swing bowling.
Guest Blog by RMIT Racing: Using Augmented Reality (AR) for R18c - Designing for the Future
RMIT Racing explains how both their combustion and electric F-SAE teams have decided to employ the use of Augmented Reality (AR) with technical support from LEAP for their 2018 campaigns, including an impressive visualisation of the aerodynamics of the R17c vehicle.
Exciting advances in Wind Engineering using ANSYS CFD
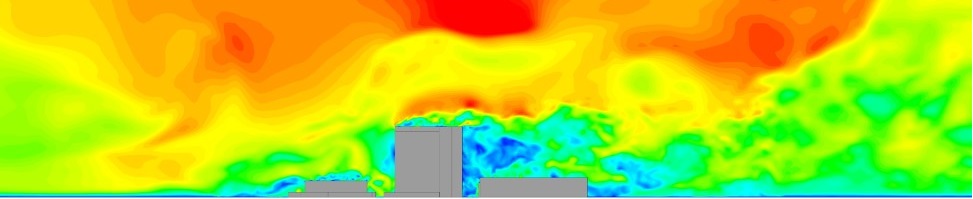
Wind engineering requires engineers to consider how a building responds to its environment as well as the effect that the structure will have on the space around it. Learn more about the use of CFD in wind engineering...
Using CFD to predict flow-generated noise and other aeroacoustic effects
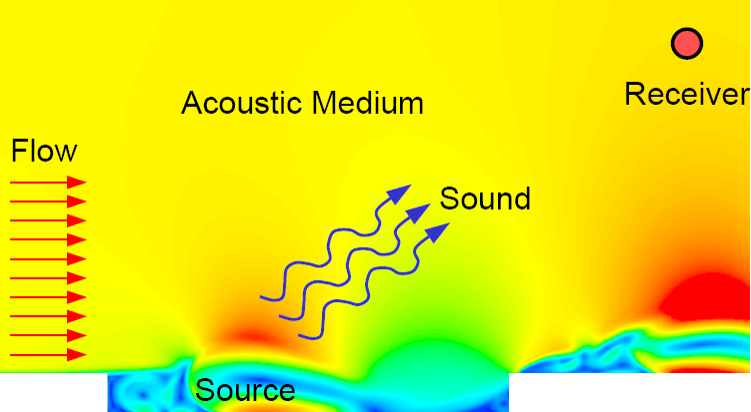
Flow-generated noise can have significantly adverse effects on our everyday lives. Product designers and engineers at the world’s most innovative and successful companies have recognised this fact, and are increasingly using CFD to incorporate noise mitigation strategies into their product design process.
Can CFD help to solve Australia’s greatest aviation mystery?
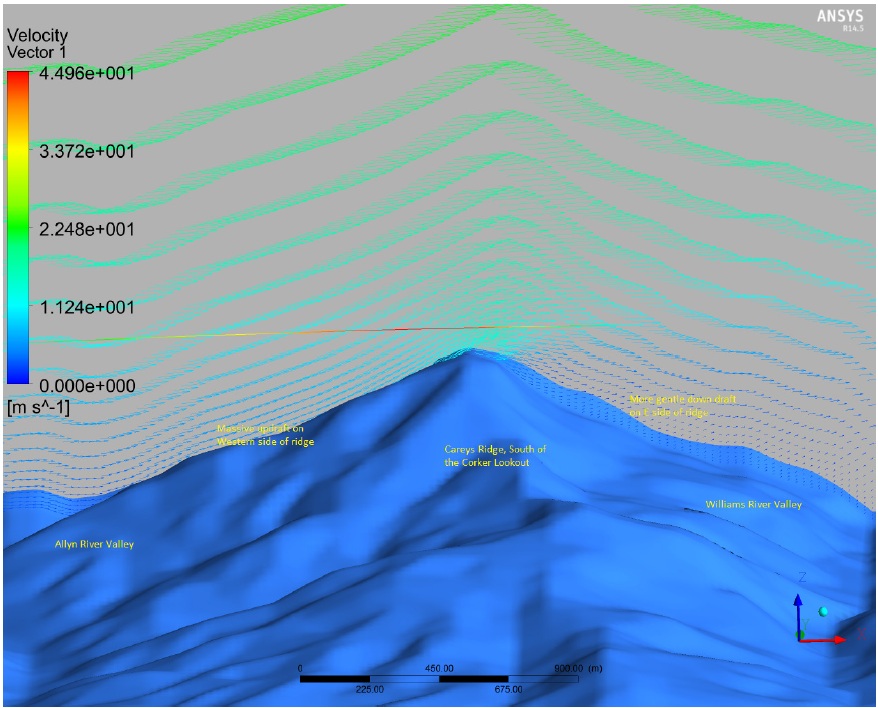
On a stormy night in August 1981, a Cessna Centurion 210 aircraft crashed with 5 people on board in Barrington Tops, a rugged and isolated national park north of Newcastle, New South Wales. Despite a massive initial search effort and ongoing attempts by a group of dedicated volunteers, the challenging and complex terrain has conspired...
Turbulence Part 5 - Overview of Scale-Resolving Simulations (SRS)
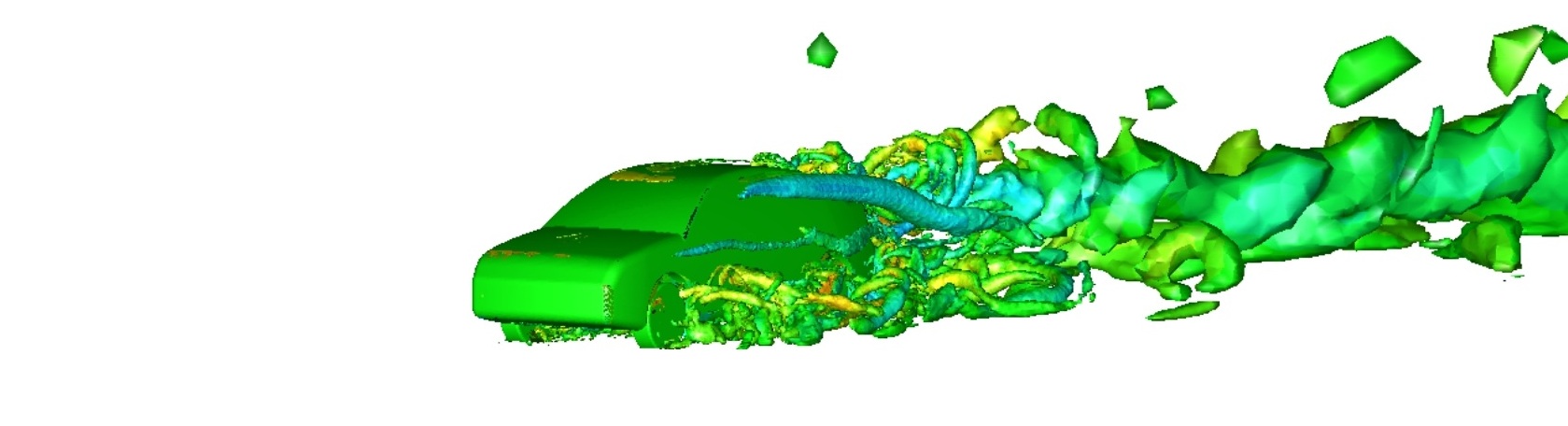
An increasing number of industrial CFD users are recognising the need to move away from RANS modelling and resolve a greater spectrum of turbulence (particularly in cases involving large-scale separation, strongly swirling flows, acoustics, etc.). Here we present an overview of Scale Resolving Simulation techniques and important considerations when considering applying SRS to your project.
Tips & Tricks: Estimating the First Cell Height for correct Y+
Turbulence Part 4 - Reviewing how well you have resolved the Boundary Layer
In recent posts we have comprehensively discussed inflation meshing requirements for resolving or modeling wall-bounded flow effects due to the turbulent boundary layer. We have identified the y-plus value as the critical parameter for inflation meshing requirements, since it allows us to determine whether our first cell resides within the laminar sub-layer, or the logarithmic...
