Ansys CFD tools in 2021 have taken another large step forward with the availability of a new product, named “Ansys CFD-Pro” - which provides our customers with the right tools to tackle a range of common CFD applications at a significantly more affordable price than the full Ansys CFD Premium package, but still using the same modern Fluent workflow, meshing technology, and core Fluent solver that has been trusted by our customers worldwide for many decades.
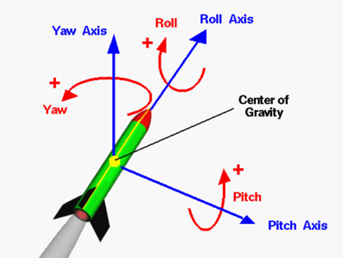
Guest Blog by USYD Rocketry Team (URT) who use simulation in their development of high-power sounding rockets to compete in the Australian Universities Rocketry Competition (AURC) and Spaceport America Cup. URT was the first Australian team to compete and took first place in the 10,000 ft COTS category with their Silvereye rocket.
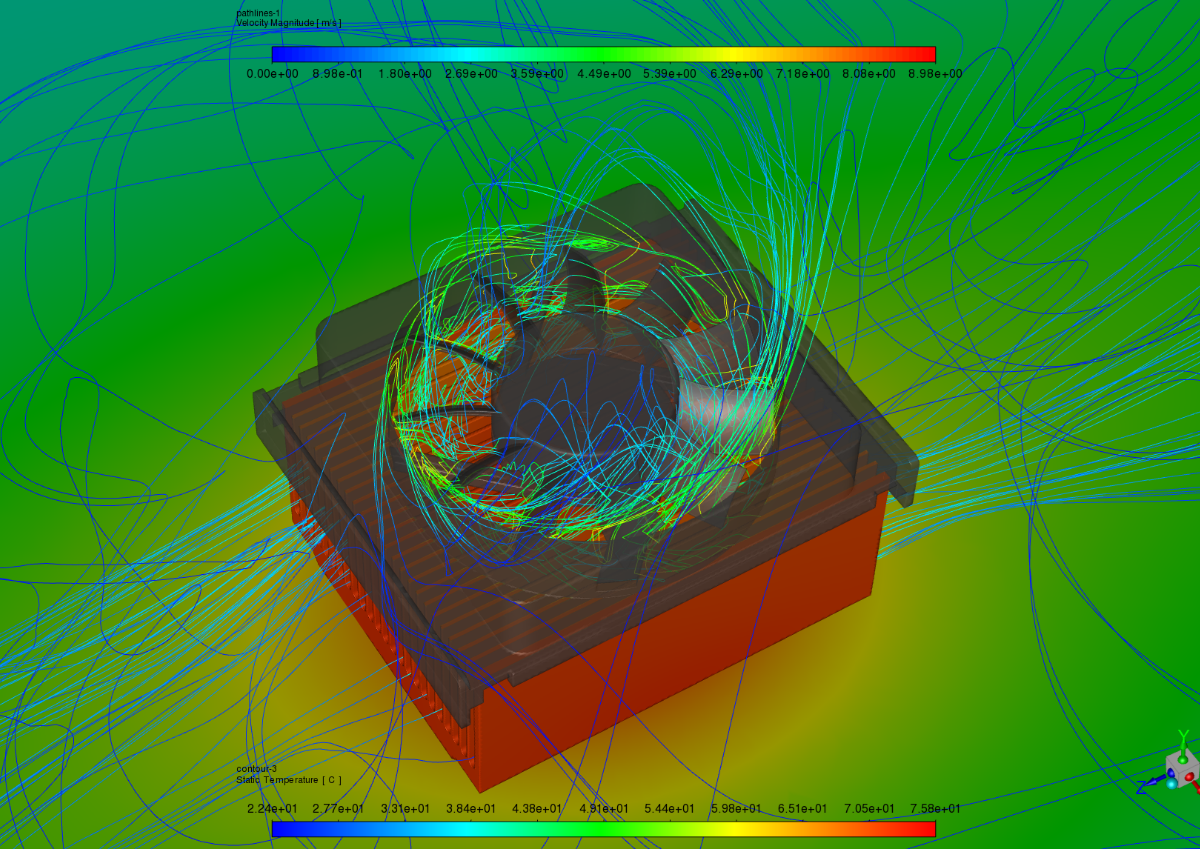
We look at recent improvements in Fluent's GUI and expressions which help streamline workflows for HVAC applications, such as those involving flow balancing, temperature monitoring and control. We apply this to an example involving two types of air handling unit for cooling a room containing heat-generating equipment.
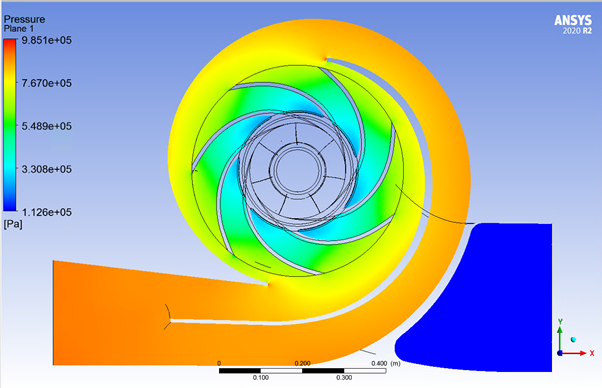
In order to improve pump efficiency, pump designers require fine-grain insights into complex fluid dynamics within a pump to help them identify areas that can be refined to reduce losses during pump operation. In this example, we look at the workflow to improve an existing pump’s design without requiring the original CAD drawings – instead using scanned data of an existing pump design.
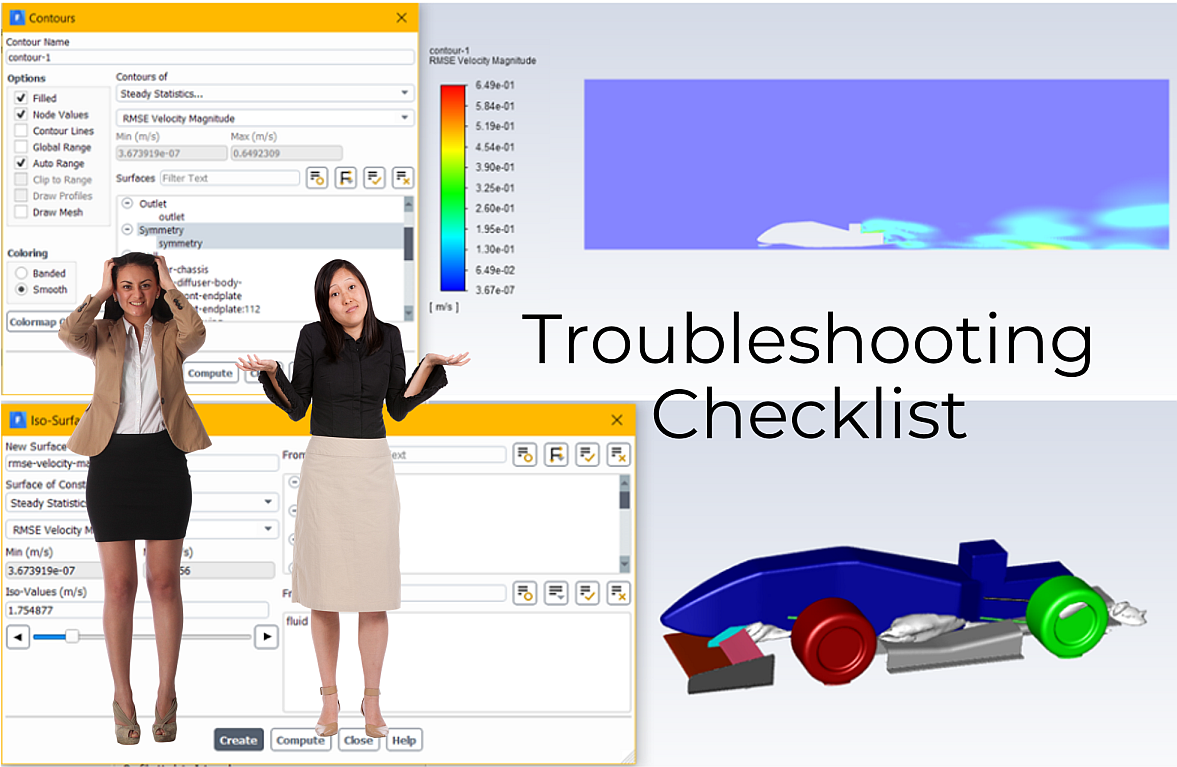
For the times when your CFD simulation is diverging or not behaving as expected, we offer a helpful checklist to systematically troubleshoot what is going wrong and successfully tackle the most challenging CFD problems.
Engineers are continually under pressure to improve the performance of their products and often look to gain an edge using optimisation techniques - trying to reduce drag, increase lift (or downforce), or reduce pressure drop. Rather than relying on intuition to make geometry changes that are often constrained (using a parametric CAD approach), you can now use the new Adjoint solver to compute localised sensitivity data (related to your objectives) and optimize your design semi-automatically.
Caravan owners are well aware that the speed they drive at and the shape of their caravan can greatly affect fuel consumption.
In partnership with Caravan World magazine, we've taken a closer look into the performance of caravans with the aid of CFD, including some less obvious factors that can help shave off the drag on your caravan and improve fuel consumption.
The water industry has a range of engineering challenges and specific regulatory requirements, especially concerning flow assurance, water quality, and even component selection. Learn how CFD delivers real value to the water industry - such as predicting complex flow behavior, across individual components or large network systems.
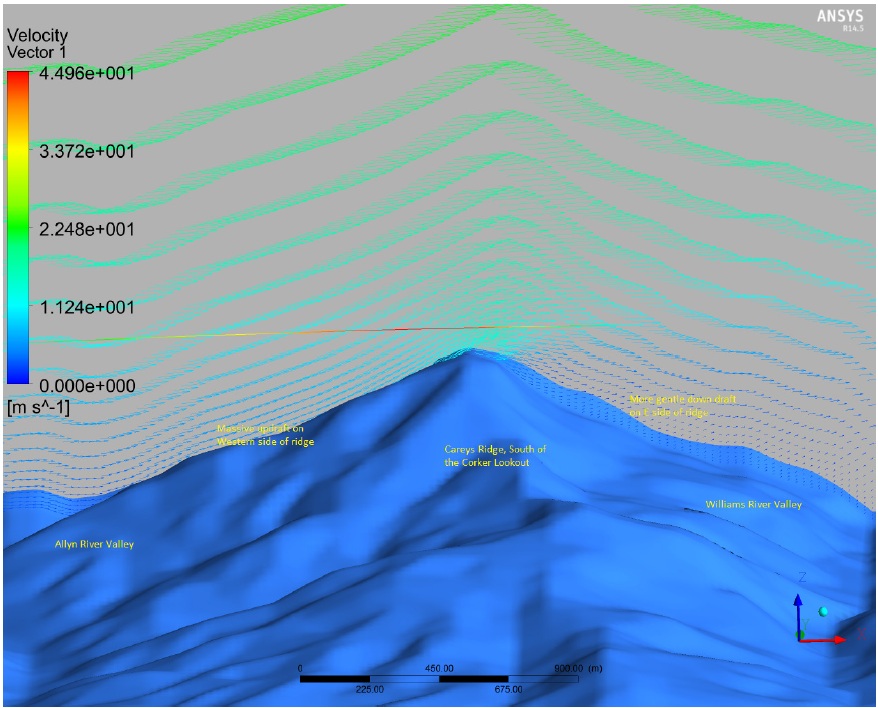
On a stormy night in August 1981, a Cessna Centurion 210 aircraft crashed with 5 people on board in Barrington Tops, a rugged and isolated national park north of Newcastle, New South Wales. Despite a massive initial search effort and ongoing attempts by a group of dedicated volunteers, the challenging and complex terrain has conspired...
LEAP staff, in particular our team of CFD engineers, have been watching with interest as the 2013 America's Cup unfolds in San Francisco. Despite being the oldest active trophy in international sport, the America's Cup is continually evolving thanks to an often dramatic combination of ...