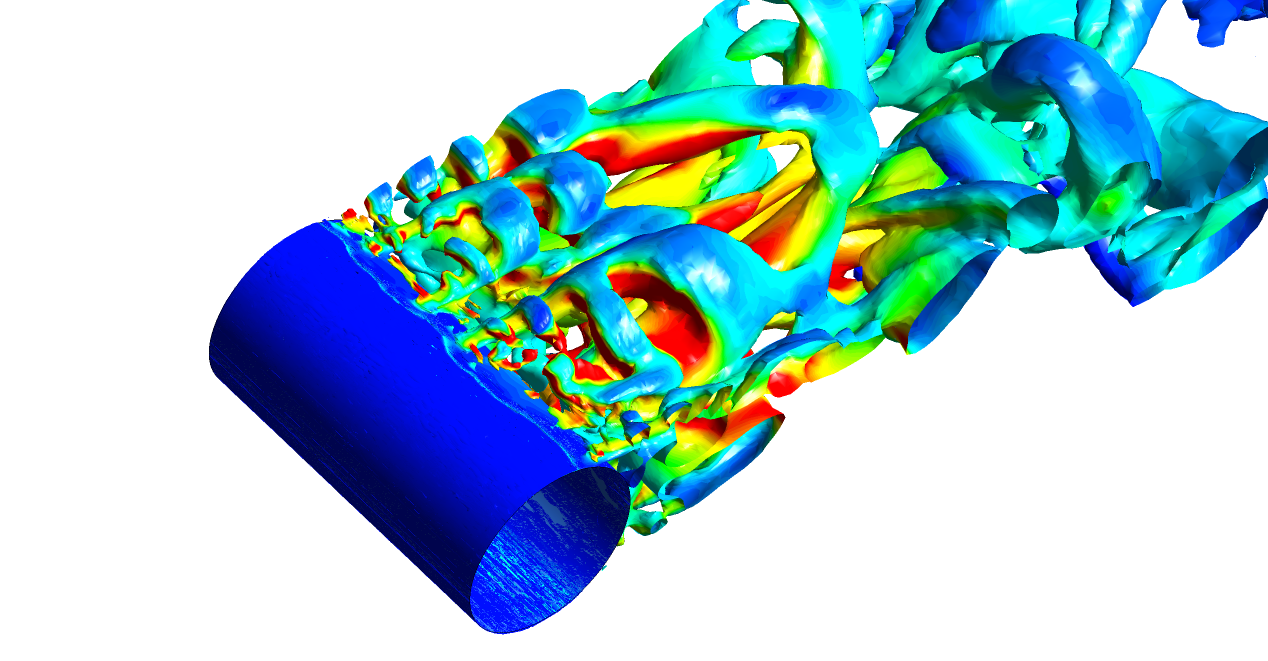
The Reynolds number (Re) is the single most important non-dimensional number in fluid dynamics and is recommended to be calculated before you begin any new CFD modelling project. The Reynolds Number is defined as the dimensionless ratio of the inertial forces to viscous forces and quantifies their relevance for the prescribed flow condition: Where U∞...
How does the Reynolds Number affect my CFD model?