The Reynolds number (Re) is the single most important non-dimensional number in fluid dynamics and is recommended to be calculated before you begin any new CFD modelling project. The Reynolds Number is defined as the dimensionless ratio of the inertial forces to viscous forces and quantifies their relevance for the prescribed flow condition:
Where U∞ and L are the characteristic velocity and length scale of the problem, ρ is the fluid density and μ is the dynamic viscosity. The use of the Reynolds number frequently arises when performing a dimensional analysis and is known as Reynolds principle of similarity. For example, air flow of U∞ = 1 [m/s] over a flat plate of L = 1 [m] will exhibit the same flow pattern as air flow of U∞ = 10 [m/s] over a flat plate of L = 0.1 [m]. This concept holds since the Re is equal and the flow is incompressible (i.e. the Mach number is low).
The Re also allows us to characterize whether a flow is laminar or turbulent. Laminar flow is characterized by lower Re and high diffusion over convection. Turbulent flow on the other hand is characterized by higher Re where inertial forces dominate considerably, resulting in largely chaotic flow. The flow may also undergo a transitioning phase whereby the flow exhibits neither completely laminar nor completely turbulent characteristics.
Free shear flow illustrating laminar, transition and turbulent phases
Note: Inertial forces are proportional to the square of velocity, while viscous forces vary linearly with velocity. Therefore as the Re → 0 it is reasonable to neglect convective terms (e.g. creeping flow). Similarly, as the Re → ∞ the viscous terms of the momentum equation can be neglected and the problem can be characterized purely by the generation of inertial forces (e.g. high supersonic and hypersonic flows).
For flows in a pipe of diameter L or non-circular pipes with hydraulic diameter L, empirical studies have shown that laminar flow occurs for ReL < 2500 and fully developed turbulent flow occurs for ReD > 4000. In the interval between, transition occurs. For external flows (e.g. flow over a flat plate), laminar flow is observed up to approximately ReD ~ 1×105 to 5×105 (where D is the distance from the leading edge) before transition to turbulence takes place and turbulent flow is observed thereafter.
Animation illustrating cyclic laminar vortex shedding
Factors influencing transition include roughness and local acceleration. The Turbulence Modelling team at ANSYS Inc, led by Dr. Florian Menter, have developed world-leading capabilities to allow CFD users to accurately model these transition effects. Using the Reynolds number, we can determine whether or not it is necessary to include transition in our simulation (as this may ultimately affect the development of the boundary layer). For example, for high speed flows over a flow plate, we may observe that the flow is predominately turbulent – in this case, transition may safely be neglected. Alternatively, for cases where laminar flow is observed for a large region of the geometry (i.e. low speed applications) then modelling fully turbulent flow may be an incorrect assumption.
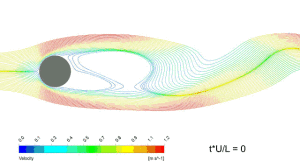
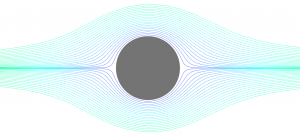
Consider the flow and wake pattern over a circular cylinder at various Reynolds numbers. At Re < 1 (see Figure 1), the flow is creeping and laminar and remains attached over the entire cylinder, which is a characteristic flow governed by momentum diffusion. At Re ~ 10 (see Figure 2) we begin to see a pair of stable and symmetrical laminar vortices in the wake. The flow in this regime is steady and the flow pattern will not change over time.
Figure 1: Re << 1 creeping flow (streamlines of velocity)
Figure 2: Re ~ 10 steady laminar flow (streamlines of velocity)
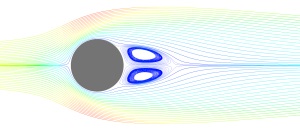
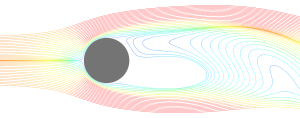
At a Re ~ 100 (see Figure 3) we see the development of a Kármán vortex street, whereby a repeating pattern of vortices are shed due to unsteady separation of the flow. While the flow is unsteady, the vortices are shed in a constant cyclic pattern and the flow remains laminar. A similar flow pattern is observed for Re ~ 105 (see Figure 4) with the exception that the flow remains laminar when it separates while the wake is largely unsteady and turbulent. In this case the use of a transition model is necessary. Assuming fully laminar flow will provide an erroneous pattern for the wake, and assuming fully turbulent flow will result in a delayed separation point (which affects the accuracy of lift and drag force prediction).
Figure 3: Re ~ 100 Kármán vortex street (streamlines of velocity)
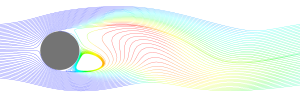
Figure 4: Re ~ 1e5 laminar flow with largely unsteady and turbulent wake (Streamlines of turbulent kinetic energy)
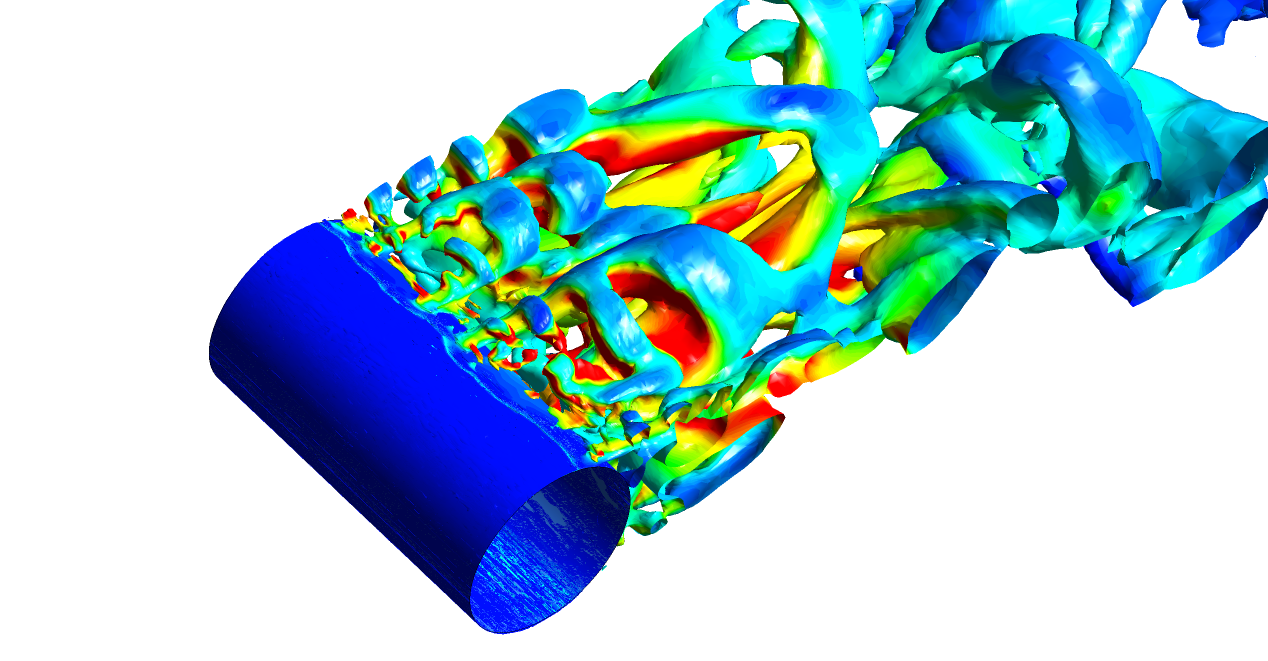
At Re ~ 106 (see Figure 5) the flow transitions to turbulence before it separates. The use of a transition model here is necessary to obtain correct viscous drag predictions but will ultimately not affect the point of separation and so we can assume that the influence of the laminar boundary layer is only additive. Furthermore, the flow can be approximated to be steady-state, as the delayed separation due to the higher stresses caused by turbulent fluctuations results in a narrower wake region. At even higher Re (while remaining incompressible - see Figure 6) a highly unsteady turbulent vortex sheet appears and instabilities in the boundary layer result in the separation point moving further upstream. This is called the trans-critical regime. This phenomenon must be captured using a high-order turbulent scale resolving simulation.
FIgure 5: Re ~ 1e6 steady fully turbulent flow field (streamlines of velocity)
Figure 6: Re ~ 5e6 three-dimensional trans-critical flow showing turbulent vortical structures
This small example should provide some basis for determining whether the use of a transition model is necessary, provided we calculate the characteristic Reynolds number and are aware of the flow pattern that we would like to capture. For further clarification, or for some insight into your own particular problem, please leave a comment below or alternatively contact our support line.
