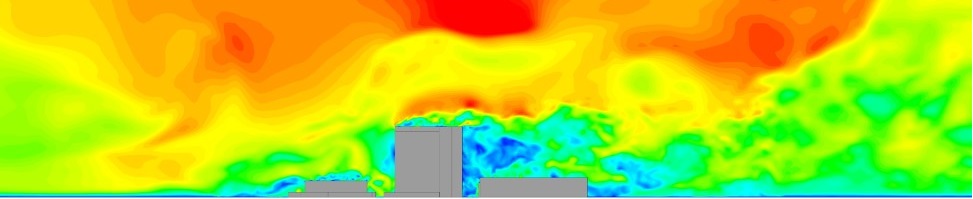
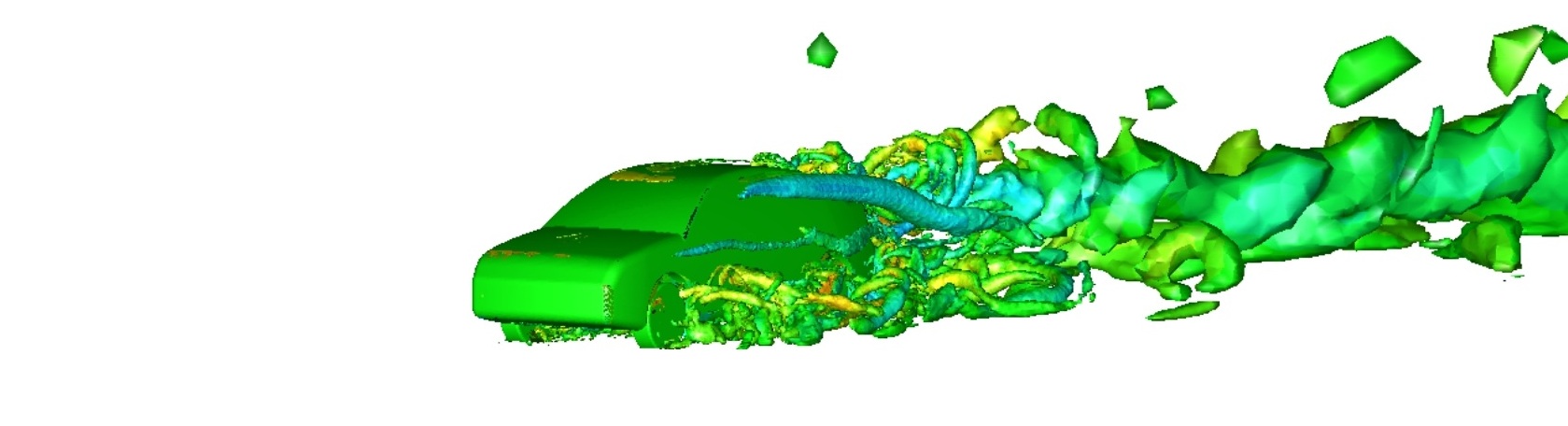
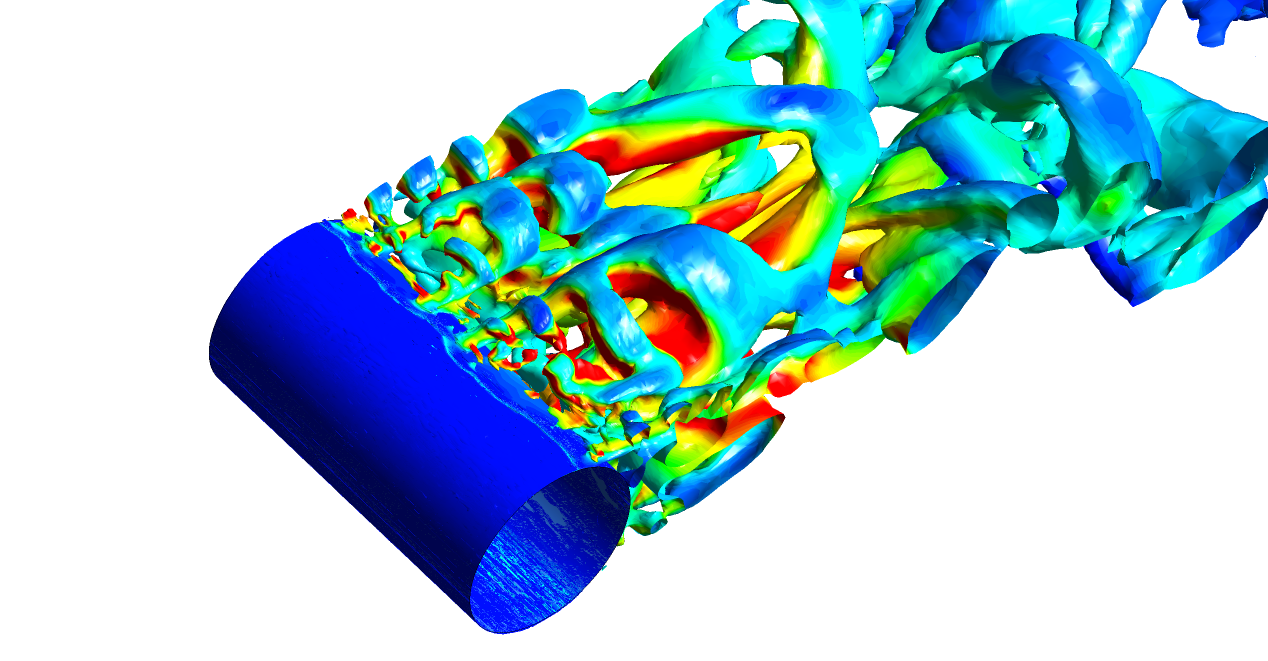
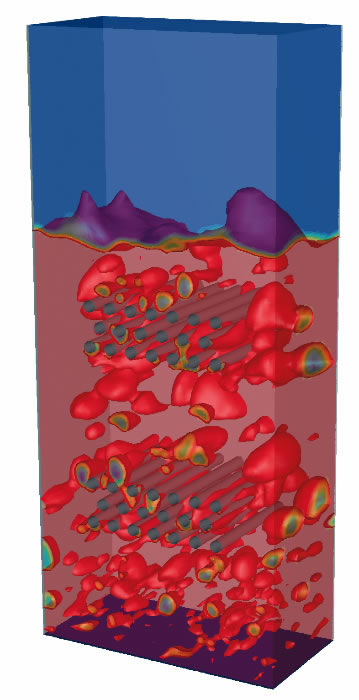
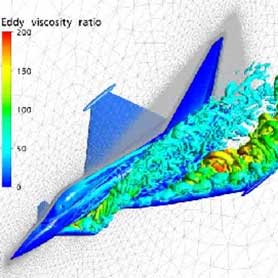
Guest Blog explaining the significance of the new Stress-Blended Eddy Simulation (SBES) turbulence approach which makes use of the best available models for both near-wall and far field accuracy, within one single scale-resolving CFD simulation, including a recording of highlights from our recent webinar.
Summary of a recent webinar presented by Prof. David Fletcher on how to take advantage of the powerful python-based expression language now available in Ansys Fluent. Examples shown included the use of expressions starting from scratch, plus examples showing how to convert your existing CFX CEL into Fluent expressions.
RMIT Racing explains how both their combustion and electric F-SAE teams have decided to employ the use of Augmented Reality (AR) with technical support from LEAP for their 2018 campaigns, including an impressive visualisation of the aerodynamics of the R17c vehicle.
The water industry has a range of engineering challenges and specific regulatory requirements, especially concerning flow assurance, water quality, and even component selection. Learn how CFD delivers real value to the water industry - such as predicting complex flow behavior, across individual components or large network systems.
Wind engineering requires engineers to consider how a building responds to its environment as well as the effect that the structure will have on the space around it. Learn more about the use of CFD in wind engineering...
Combustion technology underpins almost every facet of our modern life, from electricity generation to industrial heaters/furnaces through to automotive engines. Increasing social and economic pressure to minimise energy use and reduce pollution is driving the use of CFD to improve the efficiency of combustion processes.
An increasing number of industrial CFD users are recognising the need to move away from RANS modelling and resolve a greater spectrum of turbulence (particularly in cases involving large-scale separation, strongly swirling flows, acoustics, etc.). Here we present an overview of Scale Resolving Simulation techniques and important considerations when considering applying SRS to your project.
The Reynolds number (Re) is the single most important non-dimensional number in fluid dynamics and is recommended to be calculated before you begin any new CFD modelling project. The Reynolds Number is defined as the dimensionless ratio of the inertial forces to viscous forces and quantifies their relevance for the prescribed flow condition: Where U∞...
As we discussed in our previous post, the first step when tackling a multiphase CFD problem is to identify the key characteristics of your physical system. Once you've done this (using our checklist if you are still new to multiphase CFD), you can begin to make informed decisions on what multiphase modelling approaches to use....
As part of the visit to Australia by Dr Florian Menter, world-recognised expert in turbulence modelling, LEAP Australia is pleased to announce a webinar to be held on Thursday Aug 30th at 11am AEST. This webinar will provide an overview of recent advancements in turbulence modelling and is being held for those customers unable to...