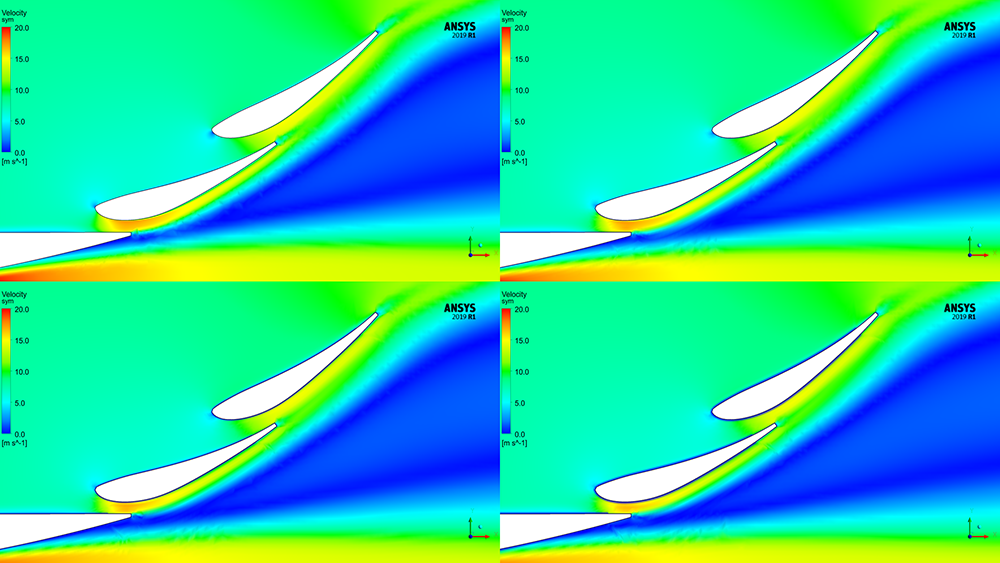
This blog provides highlights from Conflux’s presentation on their CFD heat exchange calculations at the 2021 Australasian Ansys Fluids user group. Learn how a mix of design engineers, simulation experts and additive manufacturing specialists are creating cutting-edge heat transfer solutions with the aim of revolutionising the heat exchange technologies used across many industries.
David Fletcher from LEAP discusses the importance of the 3rd Turbulence Best Practices guide recently released by Florian Menter and his team at Ansys.
This latest BPG documents the key best practices in RANS turbulence modelling, with comprehensive coverage of all widely-used 1-equation, 2-equation and Reynolds stress models.
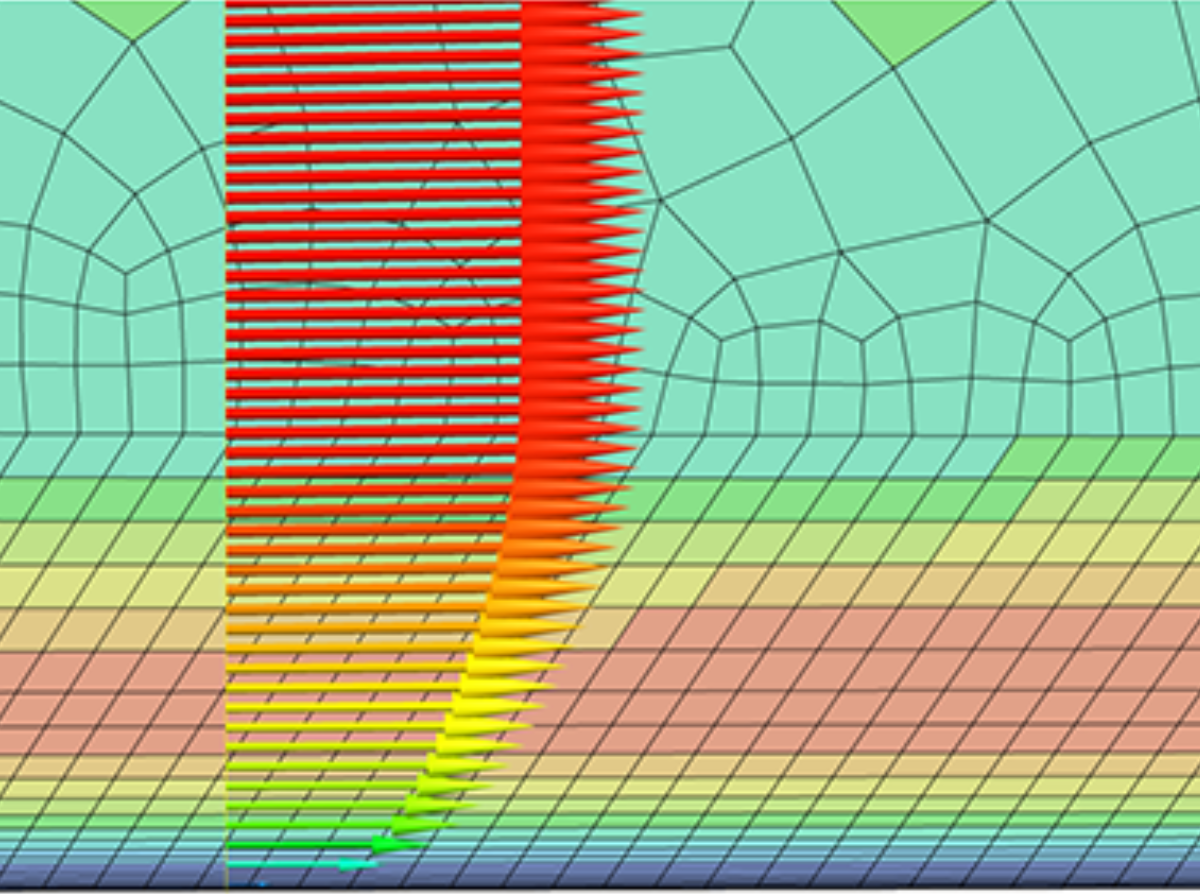
This blog series focuses on a common question: What y+ should I use in my simulations? This is the final part (Part 3) in the series – Understanding impact of Y+ and number of prism layers on flow resolution in our CFD simulations
This blog series focuses on a common question: What y+ should I use in my simulations? This is Part 2 in the series – Resolving each region of the boundary layer.
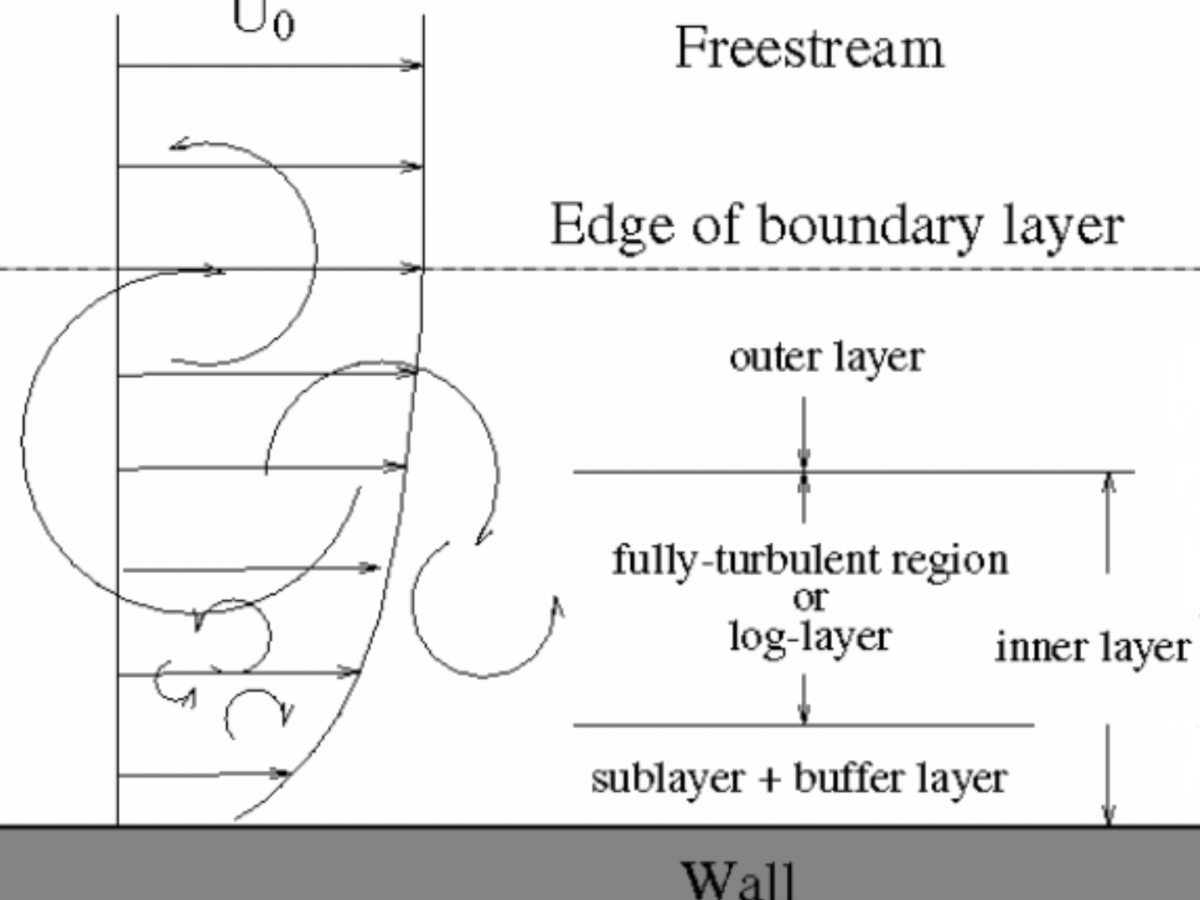
This blog series focuses on a common question: What y+ should I use in my CFD simulations? This first post is designed to help you understand the physics of boundary layers in relation to CFD meshes and Y+ values.
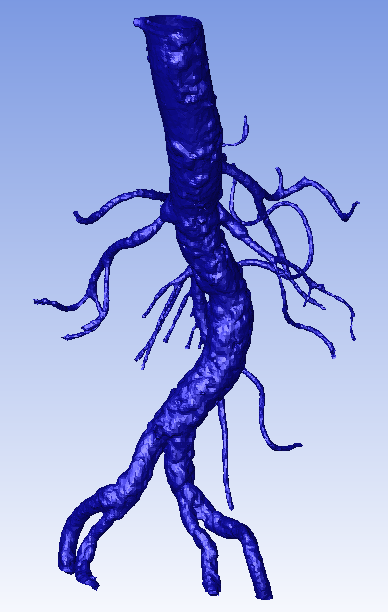
A How-To guide for Fluent Meshing's new Shrink Wrap tool which provides a powerful, easy-to-use solution for meshing complex STL geometries. This is a step-by-step guide on how to produce a high-quality CFD mesh for an abdominal aorta, imported in medium-resolution STL format (NIH).
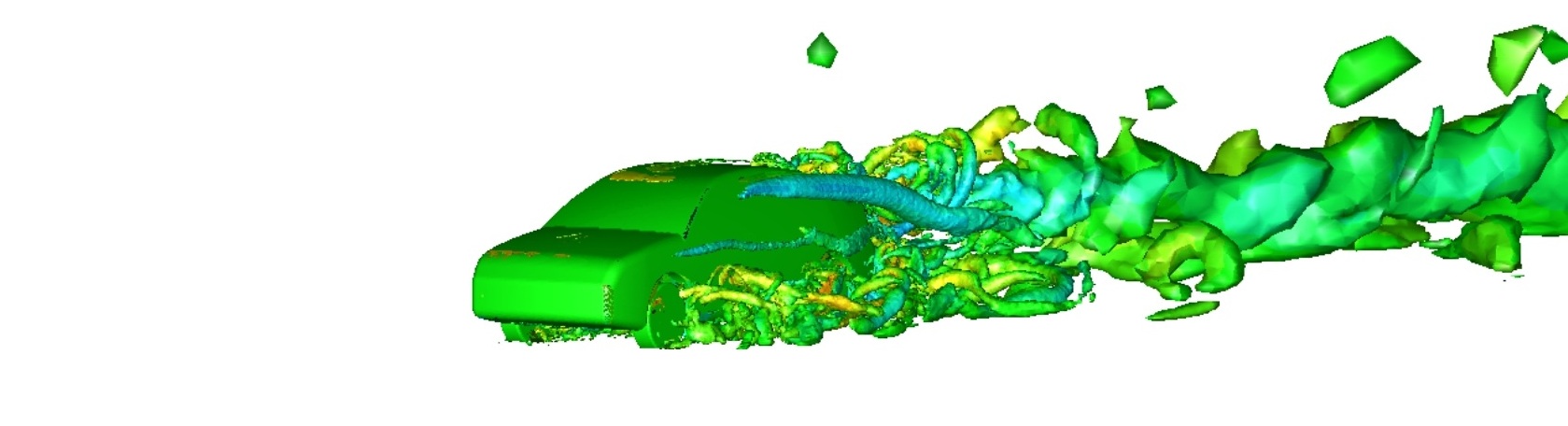
An increasing number of industrial CFD users are recognising the need to move away from RANS modelling and resolve a greater spectrum of turbulence (particularly in cases involving large-scale separation, strongly swirling flows, acoustics, etc.). Here we present an overview of Scale Resolving Simulation techniques and important considerations when considering applying SRS to your project.
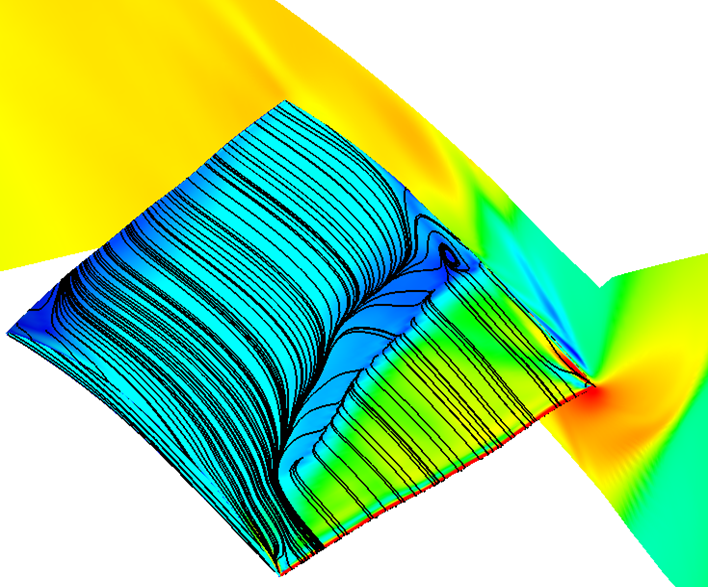
In recent posts we have comprehensively discussed inflation meshing requirements for resolving or modeling wall-bounded flow effects due to the turbulent boundary layer. We have identified the y-plus value as the critical parameter for inflation meshing requirements, since it allows us to determine whether our first cell resides within the laminar sub-layer, or the logarithmic...